Why You Should Play Bridge instead of Board Games

In graduate school, I was a board gamer. I spent many a happy Friday afternoon racing for the galaxy or building a power grid or terraforming a planet. I won more than my fair share of these outings, which contented me with the hobby until I realized it wasn’t any particular game I was good at, but the game of learning new games. Someone would introduce a new game to our group, and it was a race to decipher the latent resources, constraints, and trade-offs behind the art’s syntactic sugar. We played ad nauseam until the moment someone introduced the next game, whence the old one fell off the Earth. This game-learning game seemed to me less interesting than an actual game, at least a worthy one, so I looked for a classic to study seriously. As a mathematician with no patience for memorization (ruling out chess), I settled on bridge.

What follows is just the tiniest tidbit of tactical analysis to whet the appetite of any longtime board gamers tiring of the tabletop treadmill. It is called the principle of restricted choice. We start with a very quick description of the structure of bridge—feel free to skip the next paragraph if you’re familiar.

Bridge is a trick-taking game, in the same family as Euchre, Hearts, and Spades, played with a standard deck of 52 cards dealt out completely among four players. Each player is on a team with the player sitting opposite. Both pairs want to win as many of the 13 tricks as possible, but one pair, the declaring side, enjoys a big jump in payoff if it takes at least some number N≥7 tricks; the defenders want to stop them. There is sometimes a trump suit, which, along with N, is determined in a structured negotiation called the auction before any cards are played. One more crucial point—and one of the quirks that makes bridge so strategically deep: after the auction and the opening lead, one player on the declaring side lays his hand face up on the table. That player—the dummy—makes no decisions for the rest of the deal. Whenever it is his turn to play a card, it is chosen by his partner, the declarer.

Now suppose you hold ♠️AK2 ♥️Q2 ♦️QJ32 ♣️5432, and you find yourself as declarer with no trump suit and N=7. Your left-hand opponent (LHO) leads the ♠️3, and dummy hits the table with ♠️7654 ♥️43 ♦️54 ♣️AK1076. Remember, you are controlling both of your side’s hands and you want to take seven tricks. What do you notice?

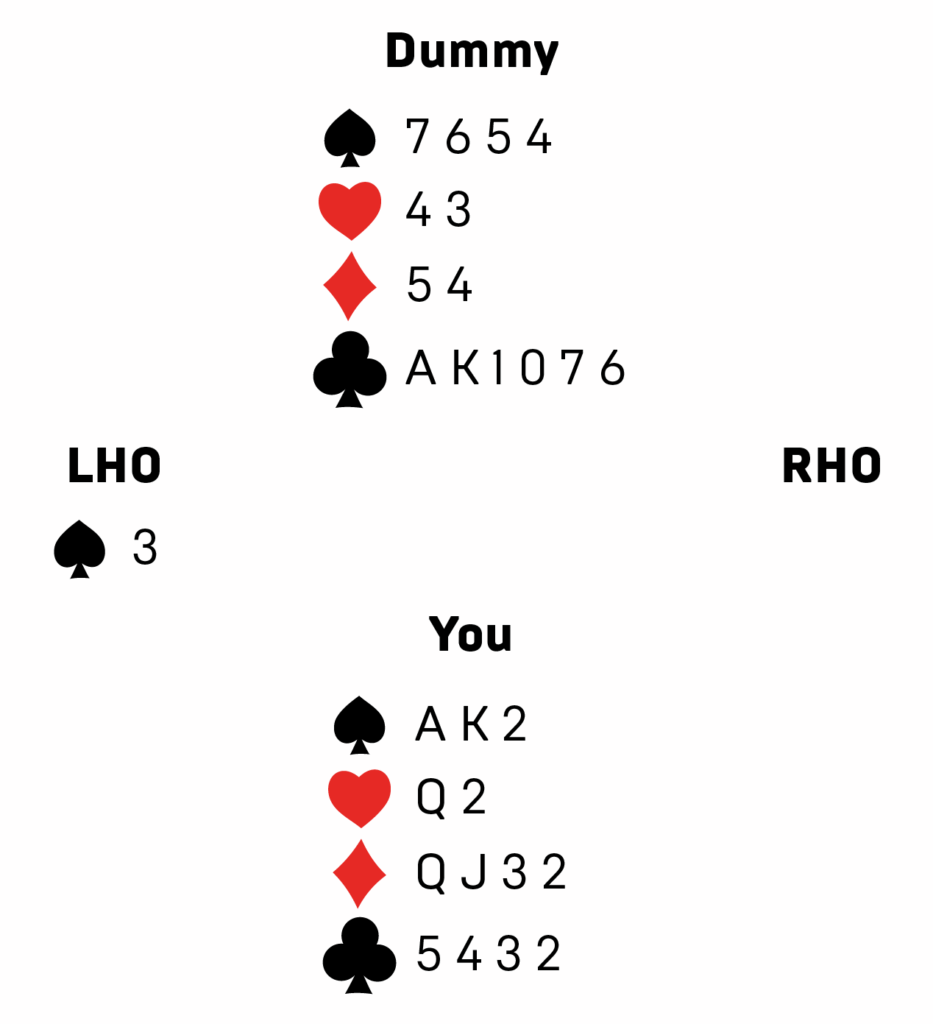
The first thing to notice is that you got lucky on the opening lead. On a red suit lead, the defenders could take at least two diamonds and five hearts before ever giving up control—enough to put you down. (Why five hearts? They have the ♥️AK between them, which will capture your ♥️Q, and one of them has at least five, which will all win tricks once both you and dummy are out of the suit.)

The second thing to notice is that you’d prefer to be playing with clubs as trump, holding nine of them together with dummy, to avoid the heartless catastrophe above. By the same token, your opponents would have done well to compete more aggressively in the auction, bidding for hearts as trump, holding most of the deck’s high cards and nine of the hearts. But here you are, sights set on seven tricks, and the rest is water under the… bridge.

And you have to take your tricks without losing the lead, because the moment you lose control, the defense can rattle off seven red suit tricks. After winning the opening spade lead in hand, your only hope is to play the club suit for five tricks. How should you do that?

There is the naive strategy of playing clubs from the top. This strategy succeeds exactly when the defenders’ collective club holding of ♣️QJ98 is divided 2-2 between them (LHO-RHO), because in exactly those cases, all four defending clubs will fall under dummy’s ♣️AK. On the other hand, if the defending clubs split 4-0, 0-4, or 1-3, you cannot succeed via any line of play (proof: exercise), so winning to all 2-2 splits ain’t bad. But can you do better? Can you win to any of the 3-1 splits? (Hint: there’s a reason I gave dummy the ♣️10!)

It turns out there is a subtler line that uses the defenders’ plays to the first club trick to decide how to play the second club trick. In this line, our default plan is the naive one—play the A and then the K—unless something surprising happens on the first round of clubs, in which case do something else. This will let us pick up two (of the four) 3-1 splits in exchange for one (of the six) 2-2 splits, making the subtler line slightly better a priori, and much better—nearly twice as good—conditioned on “something surprising.”

Let’s illustrate by continuing the play where we left off. You just won the opening ♠️3 lead in hand with the ♠️A or K. You lead any club from hand, LHO follows with one of the missing low clubs (say the 9), you call for the A from dummy, and RHO contributes the other low club. You didn’t get much information here. These defensive plays are consistent with many original holdings: Q9-J8, J9-Q8, QJ9-8, 9-QJ8. You can only possibly win to the first two, so proceed with your default plan: lay down the ♣️K and hope both defenders follow suit.

Now imagine the first club trick went differently: ♣️5, ♣️9,  ♣️A, ♣️Q! Wake-up call! This says a lot! Ignoring irrelevant splits (i.e. ignoring that RHO might be trolling us by playing the Q from QJ8, knowing he’s got us regardless), these plays are only consistent with J98-Q and 98-QJ¹. Ok, you say, but how does that help us? Here’s the key insight: holding QJ, RHO might just as well have played the J! So the cards we saw, 9-Q, come from (a) every universe of J98-Q, and (b) about half the universes of 98-QJ (we should assume²; cf. Exercise 4). Case (a), that RHO’s choice of play was restricted, is twice³ as likely!

Having thought this through, we can plan the second club trick to cater to our theory that LHO holds both remaining clubs, J8. We lead a spade from dummy and win in hand with our remaining spade honor—this step is critical, to return the lead to our hand.⁴ Finally we lead a club from hand, planning to cover whatever LHO plays as cheaply as possible in dummy (this means: if LHO plays the 8, we call for the 10 from dummy; if LHO plays the J, we call for the K). LHO follows with the 8, as expected, giving us the opportunity to err. We grit our teeth and call for the 10, knowing full well this could be fatal if RHO started with QJ—and our naive plan would have worked! When RHO discards any non-club, we breathe a sigh of relief, drop LHO’s ♣️J with dummy’s ♣️K, run the rest of the clubs, take seven tricks, and pat ourselves on the back for remembering the principle of restricted choice.

¹ RHO would not play the Q from Q8—he doesn’t know we plan to play the K next.

² Before the game, RHO picked some probability q to play the Q from QJ, if ever faced with the choice.

³ “Twice” is actually a slight lie, even assuming RHO randomizes perfectly from QJ.

⁴ Observe it would have been fatal to cash our second spade honor before playing a round of clubs!

Exercises

We claimed the restricted choice line gives up one 2-2 club split, namely 98-QJ, in exchange for two 3-1 splits. One of those is J98-Q, as we saw. What is the other?

Supply the proof that no line wins to any 4-0, 0-4, or 1-3 splits.

Footnote ¹ seems in conflict with our default plan, which was to play the ♣️K next upon seeing ♣️5, ♣️low, ♣️A, ♣️low. When (from RHO’s perspective) would it be reasonable for us not to play the ♣️K next, if he follows low?

Show that the optimal q of footnote ² is 1/2.

Explain footnote ³.

Imagine that on the first round of clubs it is LHO, not RHO, who follows with a royal: say ♣️5, ♣️J,  ♣️A, ♣️9. Do we not have the same inference as above? Why didn’t we discuss that case? Would LHO ever play the ♣️J from ♣️J8 or ♣️QJ8?

What is the best line of play if dummy’s holding is instead ♣️AQ1076?